Discretization Invariant Learning on Neural Fields

Paper | Code | Poster

Neural fields (NFs) like NeRF and SIREN are powerful representations of continuous data, but there’s a need for deep learning architectures that perform inference on such data without being sensitive to how the neural field is sampled, a property called discretization invariance.

We propose DI-Net, a general framework for discretization invariant learning on neural fields. DI-Net layers map NFs to NFs using the quasi-Monte Carlo method: they sample the input along a low discrepancy sequence and perform numerical integration with respect to some parametric map.

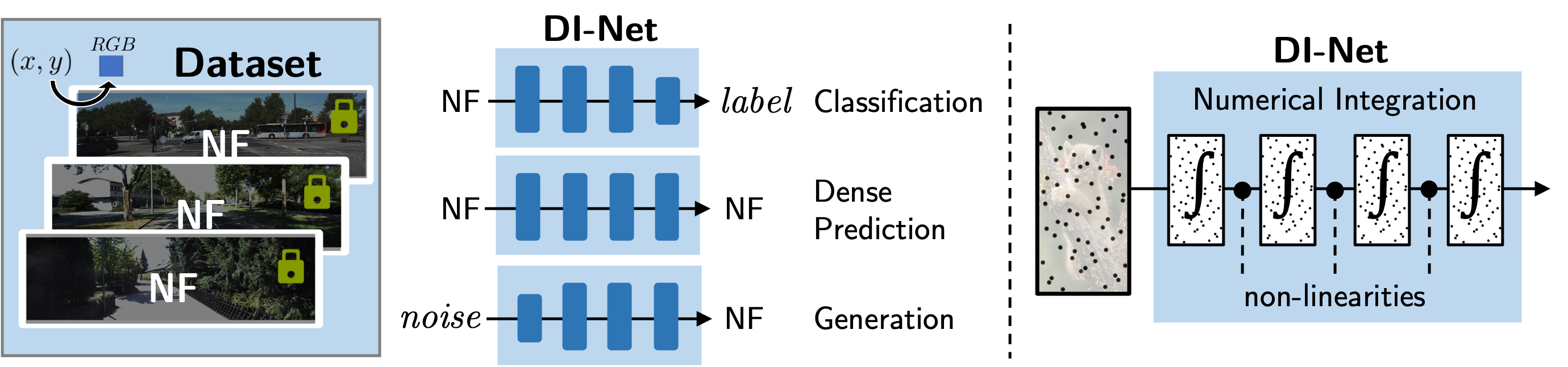
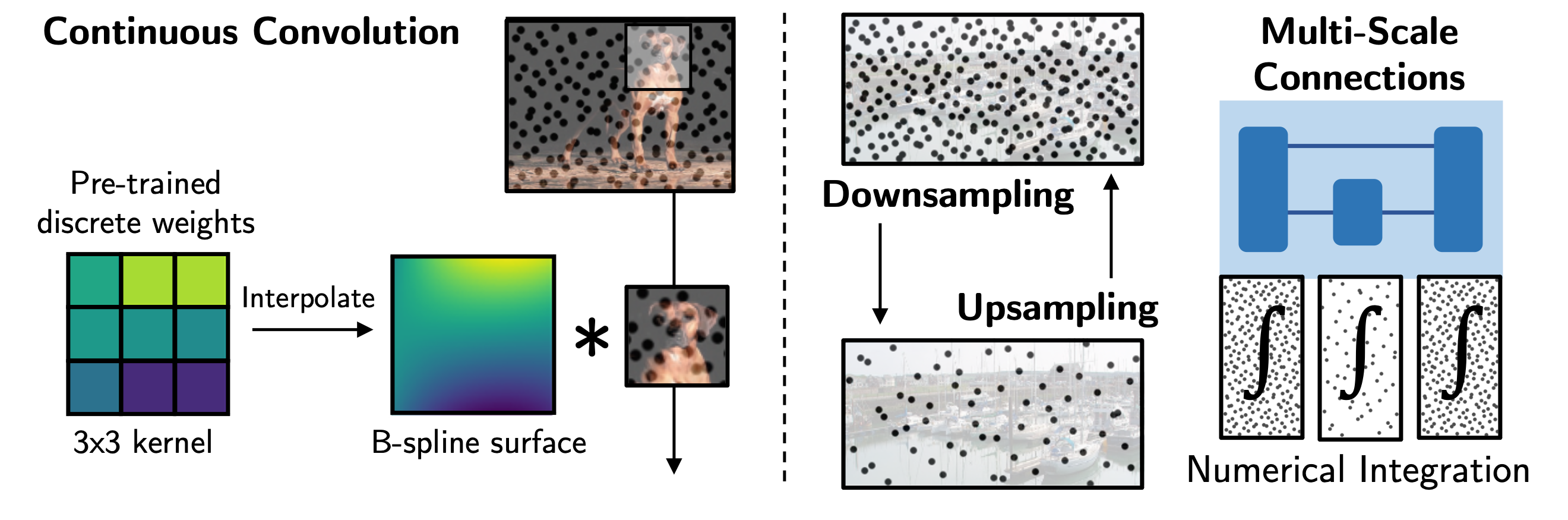
DI-Net processes a neural field by evaluating it on a point set (discretization) which is used to perform numerical integration throughout the network. DI-Nets are interoperable between all types of NFs and can be trained on a broad range of tasks.

Choosing a low discrepancy sequence minimizes the error between the discrete sample mean and the continuous integral. The parametric map can take on many familiar forms such as convolutions, attention and pooling.

DI-Nets generalize many existing network families as they bridge discrete and continuous network classes, such as convolutional neural networks (CNNs) and neural operators. They have desirable theoretical properties such as universal approximation of a large class of maps between $L^2$ functions of bounded variation, and gradients that are also discretization invariant.

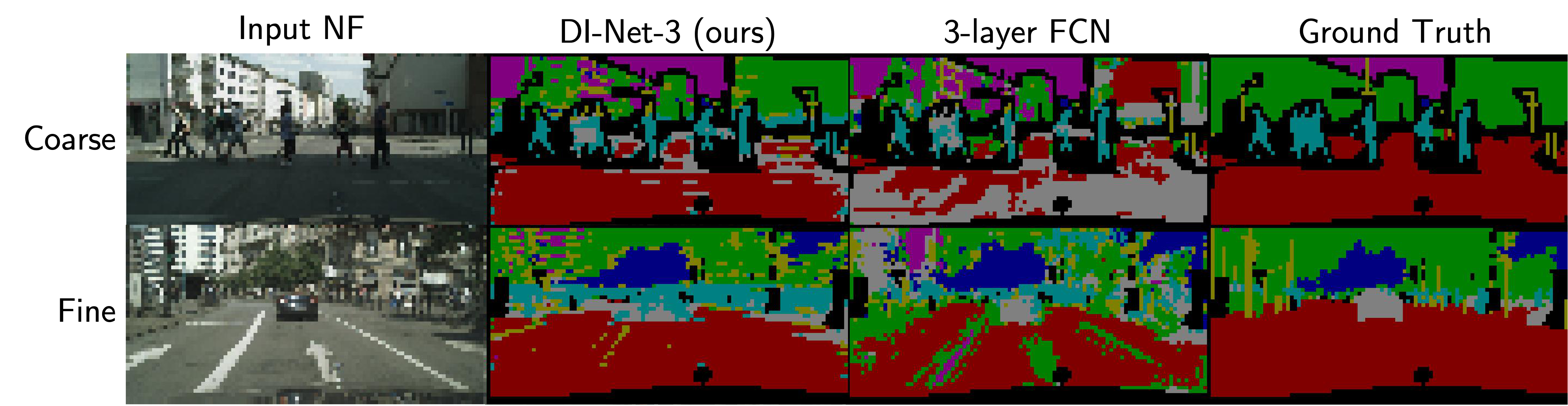
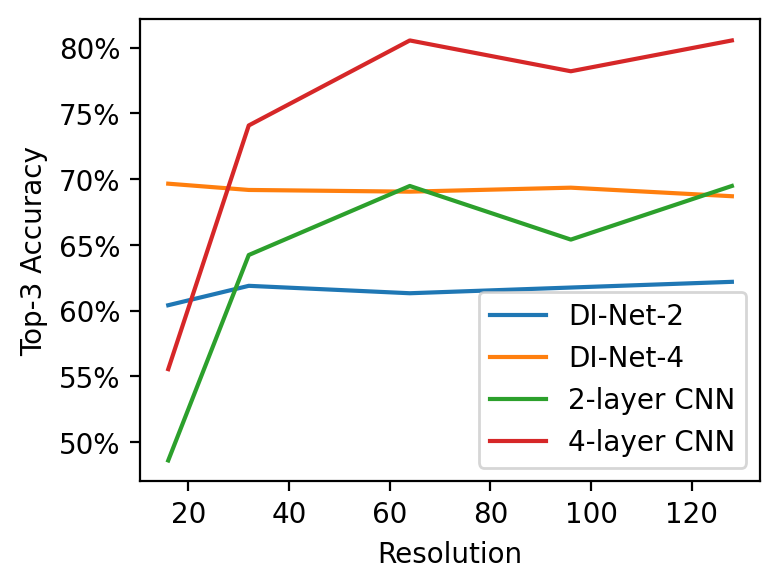
Convolutional DI-Nets generalize convolutional neural networks to arbitrary discretizations of the domain. Low discrepancy point sets used in QMC integration are amenable to the multi-scale structures often found in discrete networks. Convolutional DI-Nets may be initialized directly from pre-trained CNNs.

DI-Nets derived from CNNs can learn tasks on neural fields under various discretizations, and often generalize to new types of discretizations at test time.

Signed Distance Function Prediction

2D slices of two toy 3D scenes with signed distance functions predicted by DI-Net and a fully convolutional network.

Segmentation

Cityscapes NF segmentations for models trained on coarse segmentations only. NF-Net produces NF segmentations, which can be evaluated at the subpixel level.

Classification

Classifier performance with different resolutions at test time.

Performance under different types of discretizations at training and test time.

Train $\to$ Test Discretization	Accuracy
QMC $\to$ QMC	32.9%
Grid $\to$ Grid	30.5%
Shrunk $\to$ Shrunk	30.3%
QMC $\to$ Grid	27.1%
Grid $\to$ QMC	27.8%
QMC $\to$ Shrunk	25.4%
Shrunk $\to$ QMC	13.4%

Read our paper for more details, or check out our code

Bibtex

@misc{wang2022dinet,
      title={Approximate Discretization Invariance for Deep Learning on Implicit Neural Datasets}, 
      author={Clinton J. Wang and Polina Golland},
      year={2022},
      eprint={2206.01178},
      archivePrefix={arXiv},
      primaryClass={cs.LG}
}